講義
数値シミュレーション
有限要素法
ソースプログラムの紹介
<行列の積>
1)4行4列の行列 U、V の積 W = U × V を解くルーチン”MULT”のリスト
PROGRAM SAMPLE
DIMENSION
U(4,4),V(4,4),W(4,4)
( 4行4列の配列 U と V の値を格納 省略 )
CALL
MULT(U,V,W)
WRITE(6,10)
((W(I,J),J=1,4),I=1,4)
10 FORMAT(4E12.5)
END
SUBROUTINE
MULT(A,B,C)
DIMENSION
A(4,4),B(4,4),C(4,4)
DO
I=1,4
DO
J=1,4
C(I,J)=0.0
DO
K=1,4
C(I,J)=C(I,J)+A(I,K)*B(K,J)
END DO
END DO
END
DO
END
参考
・その他、任意の行列の積 [ N , M ]×[ M , L ] = [ N, L
]に対応したサブルーチンを考えてみるのもよい
・FORTRAN90には、行列の積を行う組込み関数MATMULが用意されているので、文献等で調べて見るのもよい。
<ガウスの消去法>
1)ガウスの消去法により連立一次方程式を解くルーチン”SOLV”のリスト
! サブルーチン副プログラムSOLV
SUBROUTINE
SOLV(C,N)
! 配列の宣言
DIMENSION
C(100,100)
M=N+1
XX=1.0E-10
DO 10
K=1,N
P=C(K,K)
P1=ABS(P)
K1=K+1
DO 20
J=K1,M
IF(P1.LT.XX) GO TO
25
20 C(K,J)=C(K,J)/P
25 DO 30
I=1,N
IF(I.EQ.K) GO TO
30
DO 40 J=K1,M
40
C(I,J)=C(I,J)-C(I,K)*C(K,J)
30
CONTINUE
10 CONTINUE
RETURN
END
2)プログラムの使用方法
ガウスの消去法により連立一次方程式
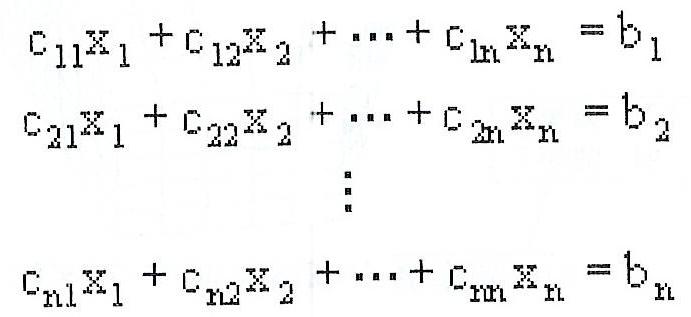
を解く。ここで上式を以下のように表す。
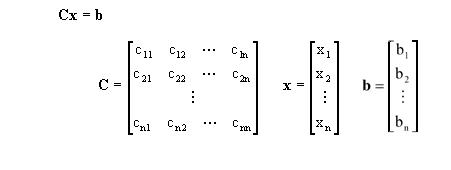
ここで b と c を下図のようにしてプログラムに組み込む。
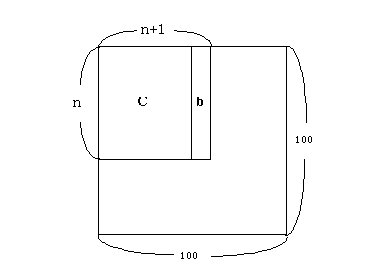
解析結果は b のところに書き込まれる。
[プログラム例]
! ガウスの消去法により連立一次方程式を解くプログラム例
!
メインプログラム
DIMENSION
C(100,100)
N=2
C(1,1)=2.0
C(1,2)=1.0
C(2,1)=1.0
C(2,2)=3.0
C(1,3)=3.0
C(2,3)=4.0
CALL
SOLV(C,N)
DO 10
I=1,N
WRITE(*,100)
I,C(I,N+1)
10
CONTINUE
STOP
100
FORMAT(' x[',I1,']=',F5.2)
END
! サブルーチン副プログラムSOLV
SUBROUTINE SOLV(C,N)
! 配列の宣言
DIMENSION C(100,100)
M=N+1
XX=1.0E-10
DO 10
K=1,N
P=C(K,K)
P1=ABS(P)
K1=K+1
DO 20
J=K1,M
IF(P1.LT.XX) GO TO
25
20 C(K,J)=C(K,J)/P
25 DO 30
I=1,N
IF(I.EQ.K) GO TO
30
DO 40 J=K1,M
40
C(I,J)=C(I,J)-C(I,K)*C(K,J)
30
CONTINUE
10
CONTINUE
RETURN
END
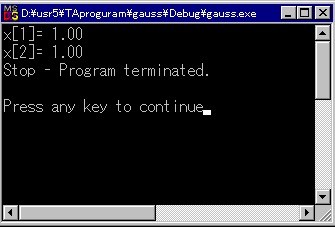
[解析結果]
トップページへ